A new isogeometric topology optimization using moving morphable components based on R-functions and collocation schemes

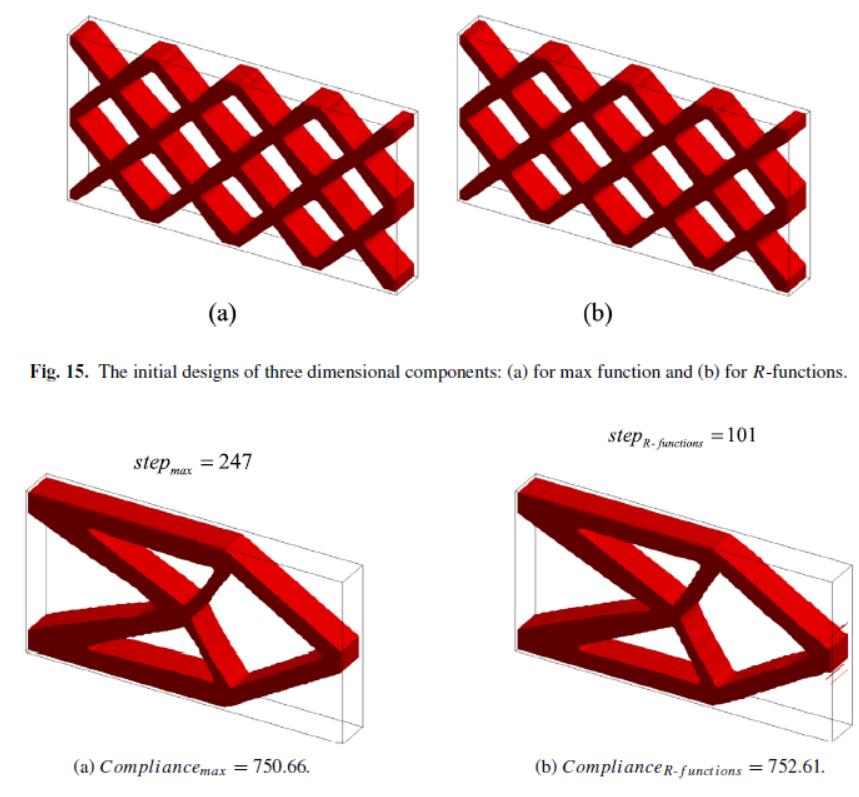
This paper presents a new isogeometric topology optimization (TO) method based on moving morphable components (MMC), where the R-functions are used to represent the topology description functions (TDF) to overcome the C1 discontinuity problem of the overlapping regions of components. Three new ersatz material models based on uniform, Gauss and Greville abscissae collocation schemes are used to represent both the Young’s modulus of material and the density field based on the Heaviside values of collocation points. Three benchmark examples are tested to evaluate the proposed method, where the collocation schemes are compared as well as the difference between isogeometric analysis (IGA) and finite element method (FEM). The results show that the convergence rate using R-functions has been improved in a range of 17%–60% for different cases in both FEM and IGA frameworks, and the Greville collocation scheme outperforms the other two schemes in the MMC-based TO.