分类： 2019

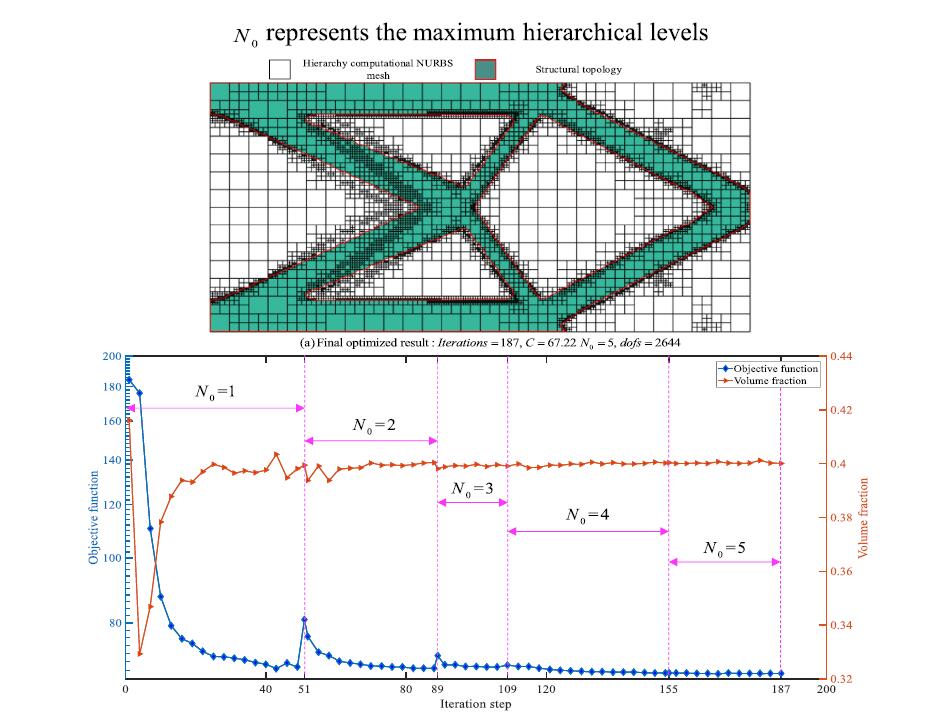
This paper presents a hierarchical spline based isogeometric topology optimization using moving morphable components (HITO-MMC). In this work, the adaptive isogeometric analysis implemented by hierarchical B-spline is adopted to efficiently and accurately assess the structural performance. An ersatz material model is derived from the Gaussian points of the hierarchy computational mesh to relate the geometric design variables with the objective and constraint of TO. To determine the iterative steps performing local refinement and the elements to be locally refined, a mark strategy is put forward based on the relative error of objective function and the value of topological description function (TDF). The mathematic model of HITO-MMC is reformulated by mapping the global displacement vector into the local displacement vector of the active elements on each level of the hierarchy computational mesh. The proposed HITO-MMC approach has twofold merits: (a) the optimization can be started from a relative coarse computational mesh and the mesh is locally refined during the course of TO, which result into
a highly computational efficiency; (b) more accurate results are obtained due to the use of high continuous hierarchical basis functions and denser mesh on structural boundary. Besides, continuous refinement is more effective to generate the optimal design than fixed NURBS mesh, and hierarchical local refinement is superior to continuous global refinement. The effectiveness of the proposed HITO-MMC is validated by a series of 2D and 3D numerical benchmarks.

This paper presents a triple acceleration method (TAM) for the topology optimization (TO), which consists of three parts: multilevel mesh, initial-value-based preconditioned conjugate-gradient (PCG) method, and local-update strategy. The TAM accelerates TO in three aspects including reducing mesh scale, accelerating solving equations, and decreasing the number of updated elements. Three benchmark examples are presented to evaluate proposed method, and the result shows that the proposed TAM successfully reduces 35–80% computational time with faster convergence compared to the conventional TO while the consistent optimization results are obtained. Furthermore, the TAM is able to achieve a higher speedup for large-scale problems, especially for the 3D TOs, which demonstrates that the TAM is an effective method for accelerating large-scale TO problems.