分类： 2016

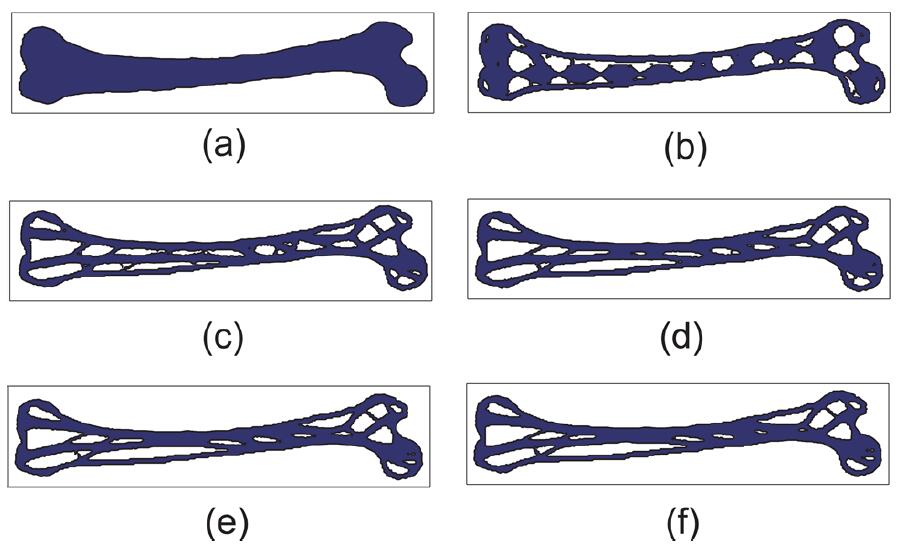
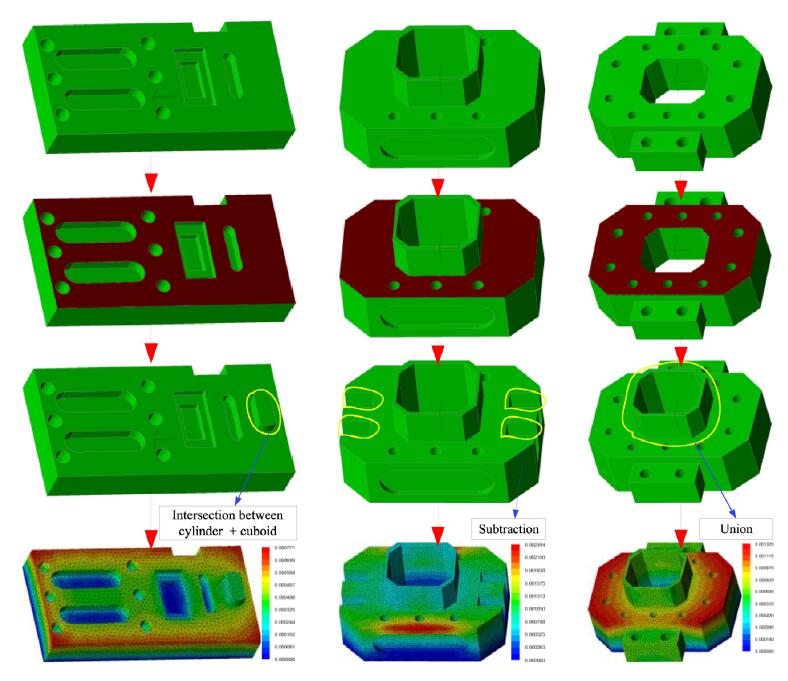
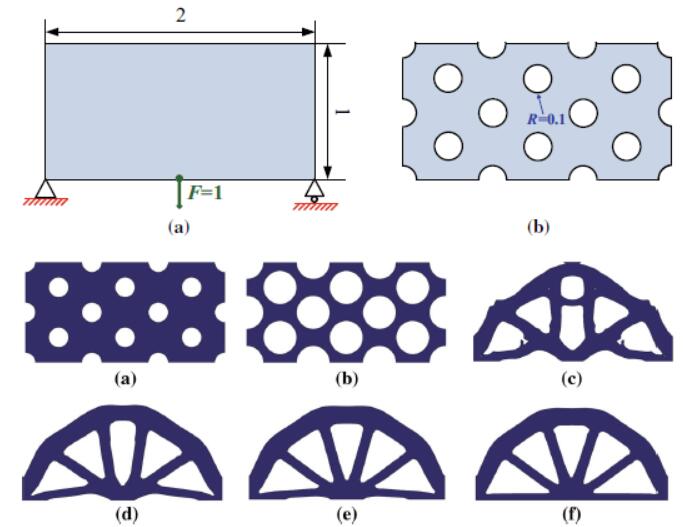
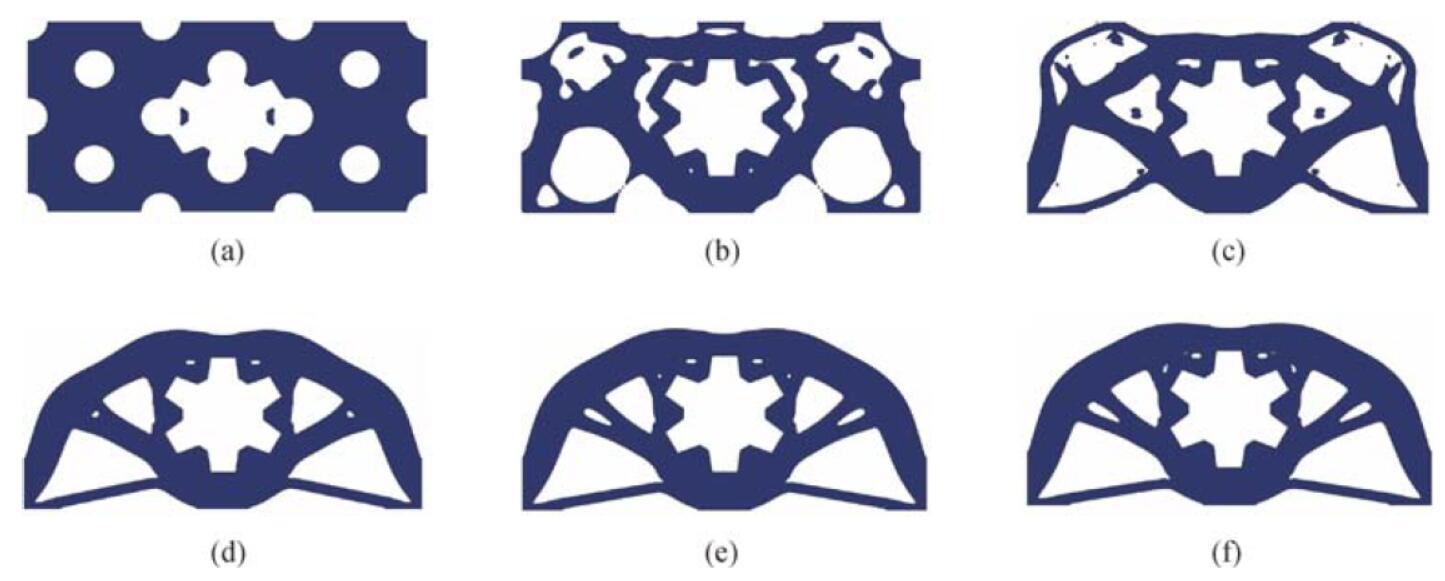
Optimization of the femur prosthesis is a key issue in femur replacement surgeries that provide a viable option for limb salvage rather than amputation. To overcome the drawback of the conventional techniques that do not support topology optimization of the prosthesis design, a parameterized level set method (LSM) topology optimization with arbitrary geometric constraints is presented. A predefined narrow band along the complex profile of the original femur is preserved by applying the contour method to construct the level set function, while the topology optimization is carried out inside the cavity. The Boolean R-function is adopted to combine the free boundary and geometric constraint level set functions to describe the composite level set function of the design domain. Based on the minimum compliance goal, three different designs of 2D femur prostheses subject to the target cavity fill ratios 34%, 54%, and 74%, respectively, are illustrated.

Boundary conditions (BCs) are important parameters of numerical computation for CAE structure analysis. Automatically and correctly reconstructing BCs would evidently improve the design efficiency. In this pa- per, a novel approach consisting of feature representation of BCs, coding mechanism for BC related topo- logical entity and BC reconstructing mechanism is proposed. BCs treated as features can be adaptive to the changing geometric model in this approach. Coding mechanism guarantees that the specified entities of BCs from the model reconstruction process could be identified. Reconstructing mechanism comprises the maintenance of BC-geometry feature dependency, data consistency and coding transmission, which ensures all the BCs can be automatically updated in terms of the changing geometry. This approach can avoid repeatedly applying BCs to the whole or portion of topological entities. Finally, some representative cases demonstrate that the proposed approach is able to significantly improve the design efficiency.

In this paper, we present an accurate and efficient isogeometric topology optimization method that integrates the non-uniform rational B-splines based isogeometric analysis and the parameterized level set method for minimal compliance problems. The same NURBS basis functions are used to parameterize the level set function and evaluate the objective function, and therefore the design variables are associated with the control points. The coefficient matrix that parameterizes the level set function is set up by a collocation method that uses the Greville abscissae. The zero-level set boundary is obtained from the interpolation points corresponding to the vertices of the knot spans. Numerical examples demonstrate the validity and efficiency of the proposed method.

In this paper, an approach based on the fast point-in-polygon (PIP) algorithm and trimmed elements is proposed for isogeometric topology optimization (TO) with arbitrary geometric constraints. The isogeometric parameterized level-set-based TO method, which directly uses the non-uniform rational basis splines (NURBS) for both level set function (LSF) parameterization and objective function calculation, provides higher accuracy and efficiency than previous methods. The integration of trimmed elements is completed by the efficient quadrature rule that can design the quadrature points and weights for arbitrary geometric shape. Numerical examples demonstrate the efficiency and flexibility of the method.