分类： 2018

Structural Design Optimization Using Isogeometric Analysis: A Comprehensive Review

Isogeometric analysis (IGA), an approach that integrates CAE into conventional
CAD design tools, has been used in structural optimization for 10 years, with plenty of excellent
research results. This paper provides a comprehensive review on isogeometric shape
and topology optimization, with a brief coverage of size optimization. For isogeometric
shape optimization, attention is focused on the parametrization methods, mesh updating
schemes and shape sensitivity analyses. Some interesting observations, e.g. the popularity
of using direct (differential) method for shape sensitivity analysis and the possibility of developing
a large scale, seamlessly integrated analysis-design platform, are discussed in the
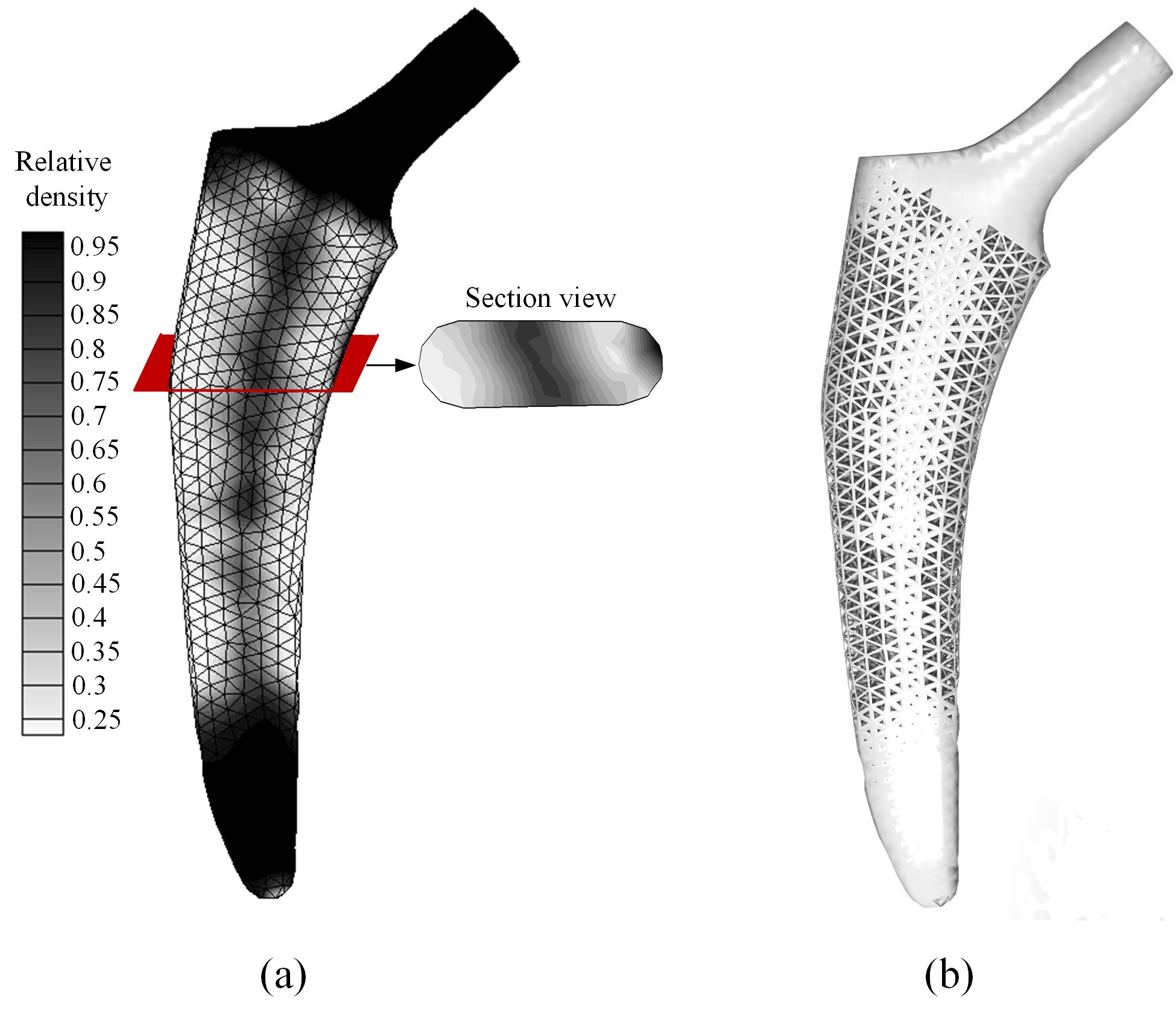
framework of isogeometric shape optimization. For isogeometric topology optimization
(ITO), we discuss different types of ITOs, e.g. ITO using SIMP (Solid Isotropic Material
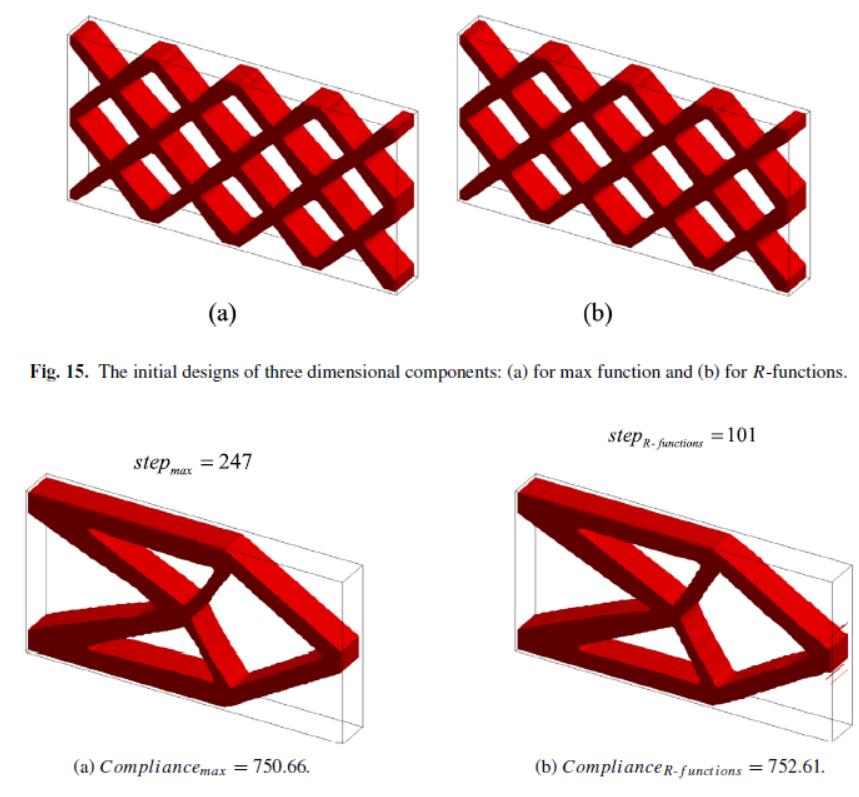
with Penalization) method, ITO using level set method, ITO using moving morphable
com-ponents (MMC), ITO with phase field model, etc., their technical details and
applications such as the spline filter, multi-resolution approach, multi-material problems
and stress con-strained problems. In addition to the review in the last 10 years, the current
developmental trend of isogeometric structural optimization is discussed.

Structural Design Optimization Using Isogeometric Analysis A Comprehensive Review-final下载

A new isogeometric topology optimization using moving morphable components based on R-functions and collocation schemes

This paper presents a new isogeometric topology optimization (TO) method based on moving morphable components (MMC), where the R-functions are used to represent the topology description functions (TDF) to overcome the C1 discontinuity problem of the overlapping regions of components. Three new ersatz material models based on uniform, Gauss and Greville abscissae collocation schemes are used to represent both the Young’s modulus of material and the density field based on the Heaviside values of collocation points. Three benchmark examples are tested to evaluate the proposed method, where the collocation schemes are compared as well as the difference between isogeometric analysis (IGA) and finite element method (FEM). The results show that the convergence rate using R-functions has been improved in a range of 17%–60% for different cases in both FEM and IGA frameworks, and the Greville collocation scheme outperforms the other two schemes in the MMC-based TO.  
CMAME-IGAMMC-2018Download

Hip implant design with three-dimensional porous architecture of optimized graded density

Even in a well-functioning total hip replacement, significant peri-implant bone resorption can occur secondary to stress shielding. Stress shielding is caused by an undesired mismatch of elastic modulus between the stiffer implant and the adjacent bone tissue. To address this problem, we present here a microarchitected hip implant that consists of a three-dimensional graded lattice material with properties that are mechanically biocompatible with those of the femoral bone. Asymptotic homogenization is used to numerically determine the mechanical and fatigue properties of the implant, and a non-gradient scheme of topology optimization is used to find the optimized relative density distribution of the porous implant under multiple constraints dictated by implant micromotion, pore size, porosity, and minimum manufacturable thickness of the cell elements. Obtained for a 38-year-old patient femur, bone resorption is assessed for postoperative conditions. The numerical results suggest that bone loss for the optimized implant is only 42% of that of a fully solid implant, here taken as benchmark, and 79% of that of a porous implant with uniform density. The architected hip implant presented in this work shows clinical promise in reducing bone loss while preventing implant micromotion, thereby contributing to reduce the risk of periprosthetic fracture and the probability of revision surgery.
2018-Hip Implant DesignDownload