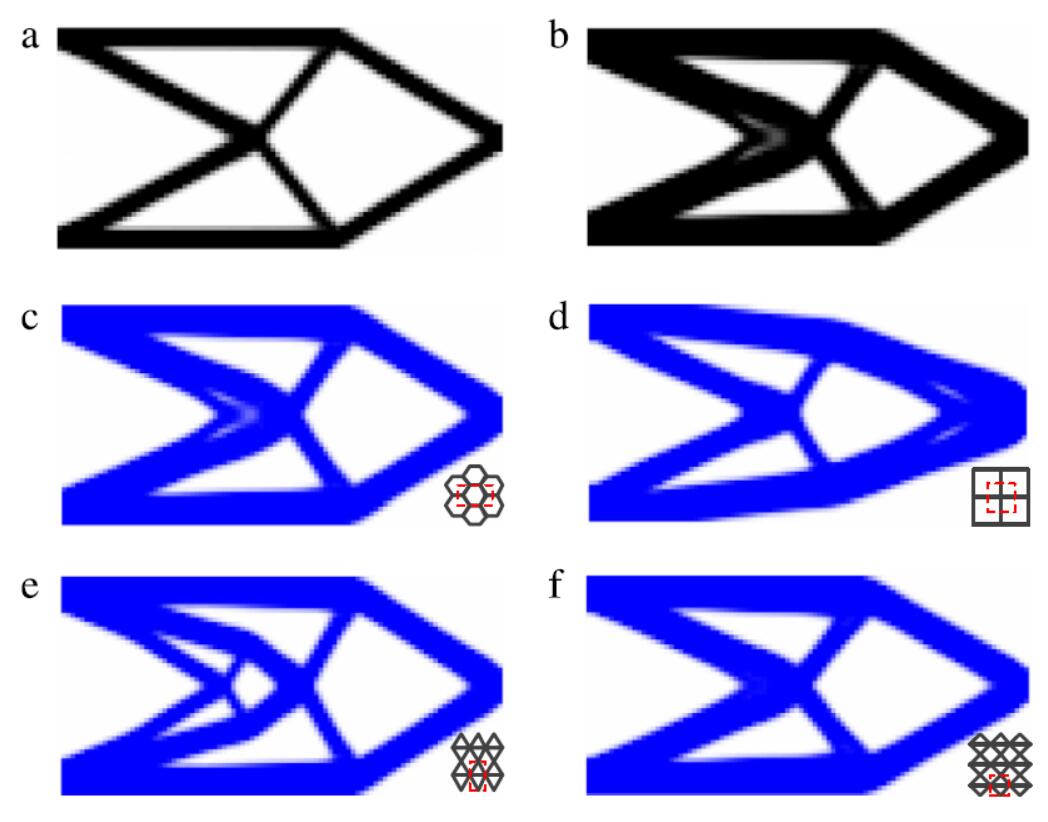
Multiscale isogeometric topology optimization for lattice materials
This paper presents isogeometric topology optimization (ITO) for periodic lattice materials, where non-uniform rational
B-spline (NURBS) basis functions of CAD models are directly used in the finite element analysis to improve computational
accuracy and efficiency. Two TO schemes that use asymptotic homogenization (AH) for the calculation of the mechanical properties
are proposed for lattice materials with uniform and graded relative density respectively. To accelerate ITO for graded lattice
materials, the mechanical properties are expressed as a function of the relative density of the unit cell, a step that avoids their
iterative calculations during ITO. Three benchmark examples are presented to validate the proposed scheme with results that show
tangible advantages, such as reduced computational time and faster convergence, of ITO over conventional TO.