An efficient isogeometric topology optimization based on the adaptive damped geometric multigrid method
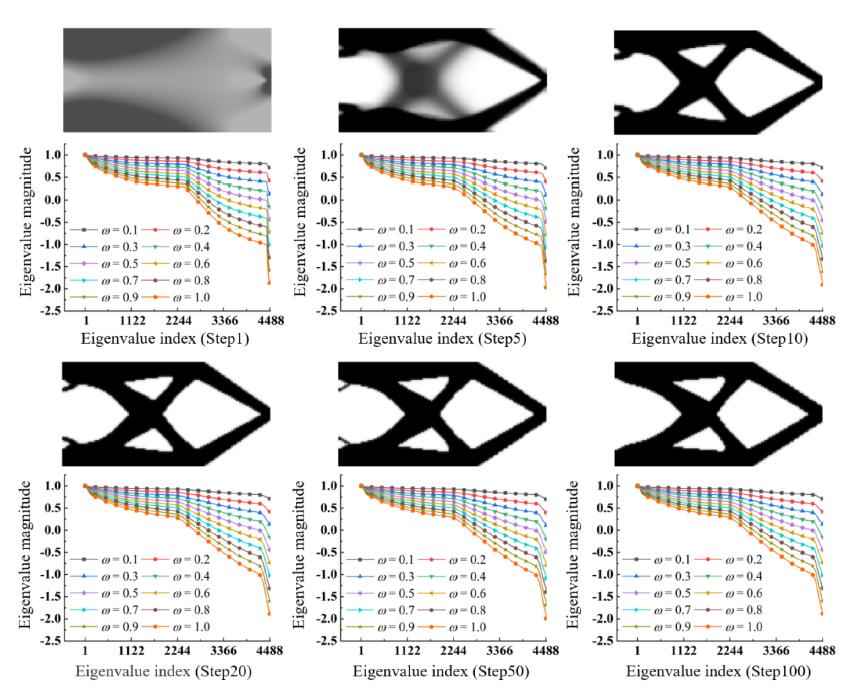
The efficiency of solving sparse linear equations in isogeometric topology optimization (ITO) can be improved by the multigrid algorithm due to its excellent convergence rate. However, its convergence rate heavily relies on the smoother’s parameters. To address this problem, a new h-refinement multigrid conjugate gradient method with adaptive damped Jacobi (ADJ-hMGCG) has been developed. By analyzing the eigenvalues of the stiffness matrix, the damping coefficient of the smoother that achieves the fastest convergence rate has been determined. Due to the significant computational resources required to compute eigenvalues in the stiffness matrix, this paper also presents a preconditioned power method based on ITO and geometric multigrid characteristics to improve the efficiency of adaptive damping solutions. The results of 2D and 3D numerical examples show that the ADJhMGCG method successfully improves the solution speed and robustness while meeting the accuracy requirements of topology optimization, and the total computational cost can be reduced by up to 59 % compared to traditional solvers for large-scale problems.