分类： 2022

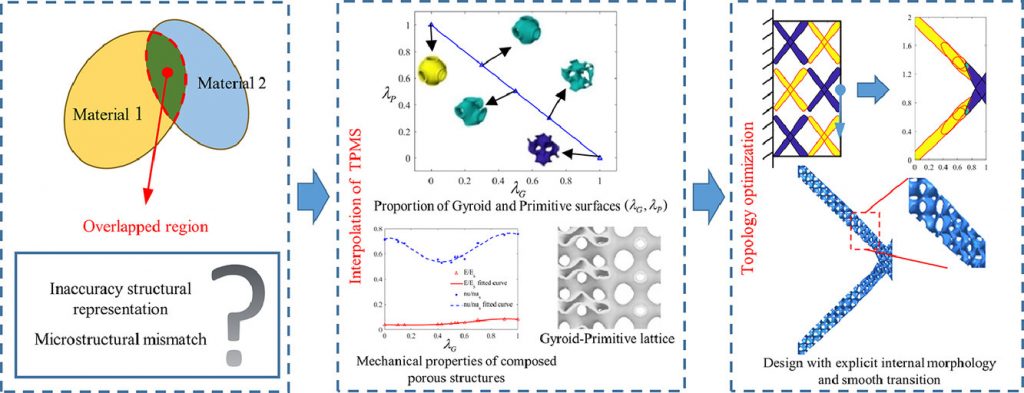
Engineering designs involving multiple materials suffer either difficult interface modeling or finding physically
meaningful transition domains with a clear or even optimal structural representation. However, previous material interpolation models often cannot achieve either of them. A new function interpolation scheme is proposed
in this work by leveraging the triply periodic minimal surfaces (TPMS). This TMPS-based architecture will serve
as the infill morphology at the microstructural scale, while its distribution at the higher structural scale will be
achieved by topology optimization (TO). The moving morphable component (MMC)-based TO is adopted to first
reduce the number of design variables and then provide explicit structural geometries. For finite elements where
multiple materials exist (or the overlapping component area), level set functions are constructed to identify the
interpolation parameters to determine the TMPS with clear material characteristics. This framework will thus
allow us to generate new architected materials associated with the optimized design variable at the structural
scale, while guaranteeing a smooth and meaningful transition at lower material microstructures. Numerical
examples show that stress concentration can be significantly reduced because of the distinguished compatibility
inside the heterogeneous structure, which leads to its successful manufacturing by the 3D printing. Finally, a real
engineering case for the design of an automotive connecting rod is presented to illustrate the versatility of the
proposed approach.

Composite materials with multiple properties are important for a range of engineering applications. Hence, this study focuses on topological design of hierarchical materials with multiple performance in both thermal insulation and mechanics. First, a novel multi-objective optimization function is defined to find a solution from the Pareto frontier, where the weight coefficients can be adjusted adaptively, to keep all the individual objective functions and their sensitivities stabilized at the same level during the optimization. Second, a new design strategy is proposed to achieve the hierarchical designs of biphasic material microstructures, they are periodically arranged by the porous base materials that are known in advance and independent of topology optimization. Third, sensitivity information and algorithm im- plementation are given in detail, and the bi-directional evolutionary structural optimization method is adopted to iteratively update the micro-structural topologies, by combining with the homogenization method. Last, numerical examples are provided to illustrate the benefits of the proposed design method, such as high efficiency, implementation easiness, good connectivity and clear interface between adjacent phases, etc.

To accelerate the structural topology optimization, this paper proposes an adaptive three- level mesh method (ATMM) to reduce the computational costs without loss of accuracy. The ATMM divides the elements into three levels: fine elements, middle elements and coarse elements. Topology optimization is initially performed on the uniform fine meshes, when adjacent fine elements change into fully voids or solids during optimization, they will merge into middle elements, and such merging processes are the same as those be- tween middle elements and coarse elements. Meanwhile, when merged middle elements or coarse elements become gray, they will return to the fine elements. To handle the incompatibility of adjacent elements in different levels, the hybrid-order serendipity el- ements are adopted. This paper proposes a new nodal numbering scheme to assemble the global stiffness matrix, and a new sensitivity filter scheme is discussed to avoid the numer- ical instability. Additionally, ATMM can obtain better acceleration and convergence, when combining with the existing gray-scale suppression technology. Lastly, four examples are provided to verify the proposed method, optimization results are consistent with those obtained from the uniform fine meshes, but with greatly reduced computational costs. In the four numerical examples, the time consumed of ATMM in each iteration is only about 30% ∼69% compared to that of the uniform fine mesh, and the total iteration numbers can be reduced by 18% ∼62%.

Auxetic materials with the counter-intuitive effect of negative Poisson’s ratio (NPR) have potentials for diverse applications. Typical shape optimization designs of auxetic structures involve complicated sensitivity analysis and a time-consuming iterative process, which is not beneficial for designing functionally-graded structures where the auxetics at different locations need to be inversely designed. To improve the efficiency of the inverse design and simplify the sensitivity analysis, we propose a deep-learning-based inverse shape design approach for tetra-chiral auxetics. First, a non-uniform rational basis spline (NURBS)-based parameterization of tetra-chiral structures is developed to create design samples and computational homogenization based on isogeometric analysis is used in these samples to generate a database consisting of mechanical properties and geometric parameters. Then, the database is utilized to train deep neural networks (DNN) to generate a surrogate model that represents the effective mechanical properties as a function of geometric parameters. Finally, the surrogate model is directly used in the inverse design framework where sensitivity analysis can be calculated analytically. Numerical examples with verifications are presented to demonstrate the efficiency and accuracy of the proposed design methodology.