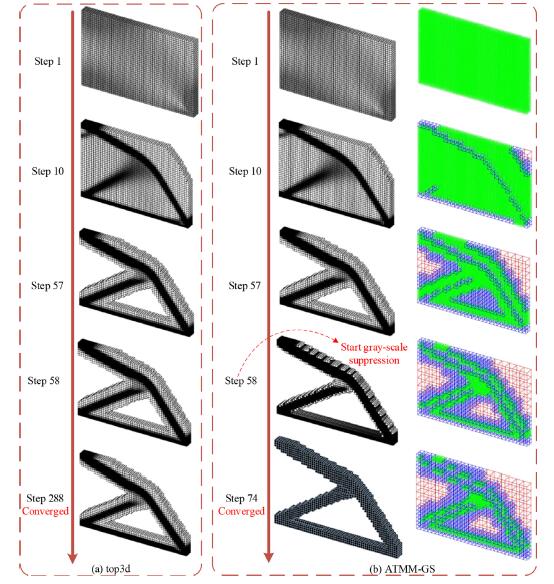
To accelerate the structural topology optimization, this paper proposes an adaptive three- level mesh method (ATMM) to reduce the computational costs without loss of accuracy. The ATMM divides the elements into three levels: fine elements, middle elements and coarse elements. Topology optimization is initially performed on the uniform fine meshes, when adjacent fine elements change into fully voids or solids during optimization, they will merge into middle elements, and such merging processes are the same as those be- tween middle elements and coarse elements. Meanwhile, when merged middle elements or coarse elements become gray, they will return to the fine elements. To handle the incompatibility of adjacent elements in different levels, the hybrid-order serendipity el- ements are adopted. This paper proposes a new nodal numbering scheme to assemble the global stiffness matrix, and a new sensitivity filter scheme is discussed to avoid the numer- ical instability. Additionally, ATMM can obtain better acceleration and convergence, when combining with the existing gray-scale suppression technology. Lastly, four examples are provided to verify the proposed method, optimization results are consistent with those obtained from the uniform fine meshes, but with greatly reduced computational costs. In the four numerical examples, the time consumed of ATMM in each iteration is only about 30% ∼69% compared to that of the uniform fine mesh, and the total iteration numbers can be reduced by 18% ∼62%.