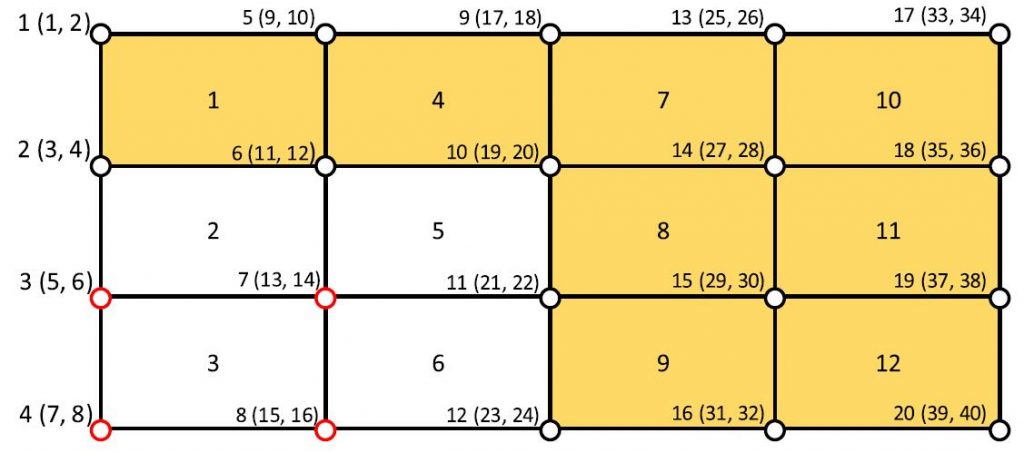
This paper proposes a highly efficient topology optimization using two accelerated methods, which can reduce the degrees of freedom (DOFs) of the finite element equations and accelerate the iteration convergence of the topology optimization. For the DOF reduction, a method based on the empty elements and the displacement change during the topology iterations is presented to remove the DOFs from the finite element equations. For the convergence acceleration, a gray-scale suppression method is proposed to accelerate the polarization of design variables which accelerates the iteration convergence of the topology optimization. Three numerical examples including 2D and 3D cases are tested, and the results show that the proposed method can significantly improve the efficiency of the topology optimization and obtain the optimization results with the same accuracy. The computational time is only about 7% – 29% compared to the conventional topology optimization method.