Acceleration of free-vibrations analysis with the Dual Reciprocity BEM based on ℋ-matrices and CUDA
Purpose
– The purpose of this paper is to present a novel strategy used for acceleration of free-vibration analysis, in which the hierarchical matrices structure and Compute Unified Device Architecture (CUDA) platform is applied to improve the performance of the traditional dual reciprocity boundary element method (DRBEM).
Design/methodology/approach
– The DRBEM is applied in forming integral equation to reduce complexity. In the procedure of optimization computation, ℋ-Matrices are introduced by applying adaptive cross-approximation method. At the same time, this paper proposes a high-efficiency parallel algorithm using CUDA and the counterpart of the serial effective algorithm in ℋ-Matrices for inverse arithmetic operation.
Findings
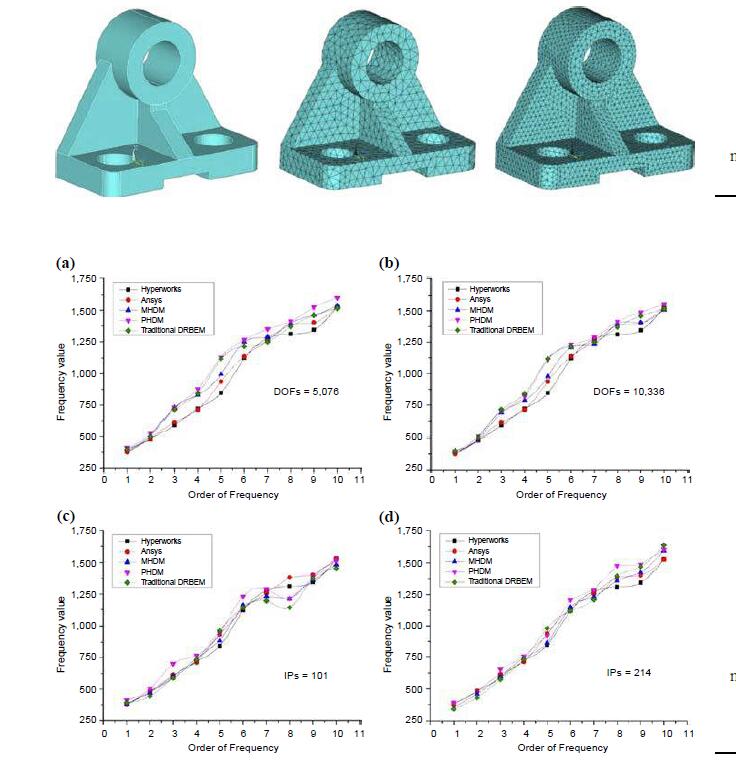
– The analysis for free-vibration could achieve impressive time and space efficiency by introducing hierarchical matrices technique. Although the serial algorithm based on ℋ-Matrices could obtain fair performance for complex inversion operation, the CUDA parallel algorithm would further double the efficiency. Without much loss in accuracy according to the examination of the numerical example, the relative error appeared in approximation process can be fixed by increasing degrees of freedoms or introducing certain amount of internal points.
Originality/value
– The paper proposes a novel effective strategy to improve computational efficiency and decrease memory consumption of free-vibration problems. ℋ-Matrices structure and parallel operation based on CUDA are introduced in traditional DRBEM.